Anisotropic Mesh Coarsening

For anisotropic problems -- including notably external viscous flow problems -- there is often a pseudo-structured part of the mesh to accurately resolve anisotropic physics. The pseudo-structured part of the mesh typically contains quadrilaterals, prisms, or hexahedra that have been divided into triangles or tetrahedra. Pseudo-structured meshes are useful in treatment of anisotropic physics, and these pseudo-structured regions should be preserved in coarse meshes to the extent feasible.

These pseudo-structured mesh regions can be coarsened isotropically, reducing the number of vertices by a factor of 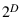$2^{D}$ in these regions by removing alternate planes of points in each direction. However, some work [5,12] suggests that multigrid methods are much more efficient if coarsening is done anisotropically, reducing the cell aspect ratio near the wall and the associated numerical stiffness. We allow several variations on anisotropic coarsening to accommodate different scenarios for surface and interior mesh pseudo-structure, as discussed in Section 6.3.1.

1. Three-dimensional meshes may have a locally anisotropic, pseudo-structured surface mesh, as shown in Figure 6.3. Roughly speaking, in this case, all fold vertices are retained, and alternate vertices are retained along closely-spaced lines leaving the fold. This process is described in detail in Section 6.3.1.
2. Both two- and three-dimensional meshes may have sections of locally anisotropic, pseudo-structured interior mesh, similar in two dimensions to the example in Figure 6.3. Pseudo-structured interior mesh fragments are coarsened in much the same way as pseudo-structured surface mesh fragments.

Selection of Points in Pseudo-structured Anisotropic Meshes

Figure 6.3: Pseudo-structured surface mesh on a wedge.

In selecting points with pseudo-structured anisotropic mesh fragments (PSAMF's) to retain in coarse meshes, we consider three important and distinct cases:

1. The fully-anisotropic case (3D). Some three dimensional meshes have anisotropic layers built out from anisotropic surface triangulations. A typical example of this is found in computational aerodynamics, where cells near aircraft wings for viscous simulations are much larger in the spanwise direction than in the streamwise direction, and much larger in the streamwise direction than normal to the wing surface. To reach unit aspect ratio in both directions during coarsening, we initially keep every point along the trailing edge in the spanwise direction, alternate lines on the wing surface, and every fourth layer in the interior of the mesh. This reduces the aspect ratio in both directions, and reduces the number of vertices by a factor of 8 in these mesh fragments. As the spanwise-streamwise aspect ratio approaches one (i.e., as the surface mesh becomes isotropic), such a mesh fragment would revert to Case 2.
2. The semi-anisotropic case (3D). Some three dimensional meshes have anisotropic layers built out from isotropic surface triangulations. In this case, we choose to coarsen the surface mesh as we would a two-dimensional isotropic mesh. In the interior, we choose to emphasize reduced cell aspect ratio near the boundary by selecting every fourth vertex along marching lines beginning at the surface vertices that will be retained. This approach reduces the aspect ratio of anisotropic cells near the boundary by roughly a factor of two at each coarsening and reduces the number of vertices in such mesh fragments by a factor of 16.
3. In two dimensions, directional anisotropic coarsening should select every fourth vertex along marching lines extending from each point on the boundary into the domain.

These rules are simple to describe and simple for a person to follow, but some care is required so that a computer can reliably identify a pseudo-structured anisotropic mesh fragment and coarsen it properly. For details, see [9].